Name That Chord!

This blog post has been triggered by questions that have arisen about chord names as a

result of my "Unique Chord Voicings" lesson series. This lesson series is currently ongoing; it's being given away for free to site members via the monthly newsletter. The lessons produced so far can be accessed by site members on the Free Lessons page (you must be a member and logged in to view). Some Unique Voicings that I teach can produce some really thorny nomenclature issues!

First of all, there is some controversy even among knowledgeable musicians about how certain chords should be named. The following is how I do it, and why. I'm going to try and be general here and not get into esoteric discussions about specific chords.

Though I'll be concentrating on the math, whenever I use a letter name I'll be on a C root. When you switch roots, the math stays the same but all the letter names change. So to avoid confusion I'll keep letter names based on C.

The Big Picture

Here is a two-octave major scale in the key of C:

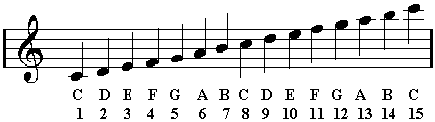
The scale degrees are numbered 1 through 15.

Chords are built by stacking 3rds. C to E is a 3rd and E to G is a 3rd. It would look like this on the staff:

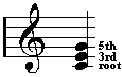
This is known as a triad (3 tones) and is the basic building block of other more complex chords. The 3 notes are the root, the 3rd, and the 5th. Any note but the root can be altered to create a different type of triad. For instance, you could flat (lower) the 3rd and that would make it a minor triad. Or you could sharp (raise) the 5th - that would make it an augmented triad. There are several types of triads and they are all created by altering the 3rd &/or the 5th of the chord. 

When a chord is called, "C" the default is major. It's a C major. If it's anything other than major, it will have something after the letter; Cm, C+, Co, Csus. Don't worry about what all these symbols mean right now; the point is that when you have a letter designating a chord, it is triadic. That is, 3 notes; there is a root, a 3rd, and a 5th. Some of those notes may be doubled; for instance, in a 1st-position open G chord on the guitar there are 6 notes but there are only 3 different notes. The root, 3rd and 5th.

Adding another 3rd gives us a 7th chord: C-E-G-B or 1-3-5-7. We've now added another alterable note so the possible types increase. Adding another 3rd gives us an 11th chord; another 3rd yields a 13th. One more 3rd gets us back to C. So in 2 octaves we've stacked up every note in the scale: C-E-G-B-D-F-A or 1-3-5-7-9-11-13.

Register Confusion

The main source of confusion about naming chords has to do with register - the lower register is the first octave; scale degrees 1 through 7. The upper register is the 2nd octave; scale degrees 8 through 14.

One example of what I call register confusion has to do with what's called open chord voicings. A close chord voicing occurs when the notes of the chord are stacked in numerical order low to high: root, 3rd, 5th - they are as close as they can be. Sometimes the voicing is opened up - the 3rd is raised an octave so the voicing is now root, 5th, 3rd. Theoretically, the 3rd is now the 10th because it's in the higher register, but it's still understood to be the 3rd of the chord. Open voicings disregard register when numbering the notes of a chord.

The guitar, because of the way it's tuned, is by default an open-voiced instrument. Most chords beyond triads (7th chords, 9th chords, 13th chords) are usually open voicings. There are close voicings for these extended chords (7ths, 9ths 13ths) common on the guitar, but they usually omit either the 5th, or the root.

Another example of register confusion has to do with the fact that the letter names are the same in every register even though the numbers are different.

In terms of letter names (remember we're on a C root):

• 2 equals 9 - both the 2nd and 9th degrees of the scale are D. Another way to put it is the 9th is the octave of the 2nd.

• 4 equals 11 (F) The 11th is the octave of the 4th.

• 6 equals 13 (A). The 13th is the octave of the 6th.

Is it a 6 or 13 Chord?

So, for instance, C6 would consist of C E G A - 1 3 5 6. If there is a 7th in the chord then the 6th (A) would be a 13th even if it's in the lower register. So if your chord is spelled (low to high) C E G A B the A would be a 13th, not a 6th, even though it's in the lower register below the 7th. Whether or not the A is a 6th or a 13th is determined by whether or not there's a 7th in the chord. If the chord is open-voiced and spelled, C G E A, it's a C6 because there's no 7th in the chord - even though the A is in the upper register, which is a 13th away from the root.

Is it a Suspended or an 11 Chord?

There are even more issues when it comes to 11th chords and - again - they mostly stem from register confusion.

Whether or not an F is an 11th or a 4th (or a suspended 3rd) on a C root is determined by whether or not there is a 3rd in the chord. If there is a 3rd in the chord then it's an 11th. If there's not a 3rd in the chord it's a 4th - more accurately a suspended 3rd. C7sus has a root, #3(4), 5 and 7 - or spelled: C F(#3/4) G(5) Bb(7). If the chord has a root, 3rd(E), 5th and 7th with an F in there somewhere then the F is an 11th, not a 4th - no matter the register.

(NOTE: C7 has a flatted 7th (Bb) - it's called a Dominant chord type. If the 7th was a B natural it would be named Cmaj7 - a full understanding of 7th-chord nomenclature can be had from Unit 4: 7th Chords.)

In spite of the above, it's very common to see a C11 symbol when a C7sus is intended. In my opinion, that's a wrong nomenclature. C11 would include an E (the 3rd) and thus is not a suspended chord.

Things get even fuzzier with sharp 11/flat 5 chords. The sharp 11 is the octave of the b5. Theoretically, if consistency is to be maintained, a sharp 11 chord would include the 5th. But as far as a Dominant chord goes, it hardly ever does. So there's really no functional difference between a C7(#11) and a C7(b5). This is even more so on the guitar, where the sharp 11 and the 5th are usually but a 1/2 step away from each other, by virtue of the fact that the chord is almost always some kind of open-voicing. Thus, on the guitar, you hardly ever have a 5th and any kind of 11th in the same chord. Having said that, some of my Unique Voicings do have both - that's one of the reasons they're unique!

What About 9th Chords? Add 2 Chords? Sus 2 Chords?

Much like suspended chords there are multiple issues that stem from register confusion.

Remember that 2 = 9!

If the chord symbol says C9, that is a 7th chord (root, 3rd, 5th, 7th) with a 9th added. If the chord symbol is Cadd9 or C(add9), there is no 7th - it's a C triad with a 9th added. Sometimes a chord is nomenclated, Cadd2. Functionally, that's the same as Cadd9. It's a C triad with a 2nd added. In my opinion, it should be nomenclated Cadd9 but I'll grant Cadd2 as also (nominally) correct - especially if the D (which can be the 2nd or the 9th) is in the lower register.

Sometimes you'll see Csus2 when Cadd9 or Cadd2 is intended. In my opinion, this is wrong; the word sus is an abbreviation for suspended. When something is suspended it is raised. A suspended (sharped) 2nd is not what's intended - add 2 or add 9 is the correct nomenclature.

Sometimes you'll see C2 when Cadd9 is intended. C2 is not a chord, it's an interval. The ubiquitous power chord, otherwise known as the 2-note rock chord, is written as C5. C is the root, and the 5th note of the scale is added - it's an interval of a 5th. Likewise, C2 would be an interval of a 2nd. The knowledgeable musician must just deal with the misnomer - Cadd9 is what's usually intended by C2.

Conclusion

This has been a general overview of the subject. The main takeaway I want you to get from all this is:

2 = 9

4 = 11

6 = 13

On a C root:

• If there's a D in the chord it's almost always a 9th.

• If there's an F(4th) in the chord and no E(3rd), the F is usually a sharped 3rd, otherwise known as a suspension. If there is both an E(3rd) AND an F in the chord, then the F is an 11th, not a 4th, nor a suspension (sharped 3rd).

• If there's an A in the chord, but no B(7th), then A is the 6th. If there's a B(7th) in the chord, then the A is a 13th.

I will now open myself up for the inevitable arguments!

Contact Jay - or reply in the comments section below if you want the discussion public.

---

Check out Master Guitar School!

Sign up as a Master Guitar School site member - it's free! - and get access to dozens of free site-based lessons, a monthly newsletter that contains a brand-new free lesson, and DEEP discounts on lesson series downloads - plus more!

Leave a comment and share through your social networks using the links below!